| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- convexhull
- c언어
- #English
- #실생활 영어
- python 알고리즘
- #프로젝트
- python __init__
- 이미지 생성
- #Android
- word embedding
- tokenizing
- 영어
- 딥러닝
- object detection
- text2img
- #영어
- #opencv
- tensorflow update
- TensorFlow
- #실생활영어
- keras
- findContours
- opencv SURF
- 영어명언
- #1일1영어
- #영어 명언
- python list
- 완전탐색
- Convolution Neural Network
- #일상영어
- Today
- Total
When will you grow up?
python_그래프 기초 본문
그래프(graph)는 여러 노드(node or vertex)들이 간선(edge)으로 연결된 추상 네트워크를 말한다.
즉, 그래프는 노드+간선의 집합으로 정의된다.
수식 - G=(V,E) V: vertex의 유한 집합, E: 간선 집합
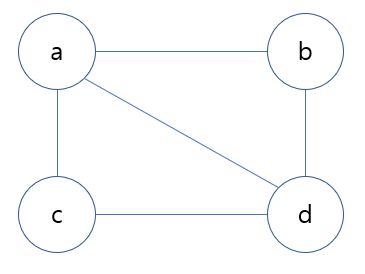
그래프 방향
그래프는 방향이 있는 그래프(directed)와 방향이 없는 그래프(undirected)가 있다.
방향이 있는 그래프는 간선에 방향이 지정되어 있지 않아, 서로 인접(adjacent)해 있으며, 이웃(neighbor)이라고 한다.
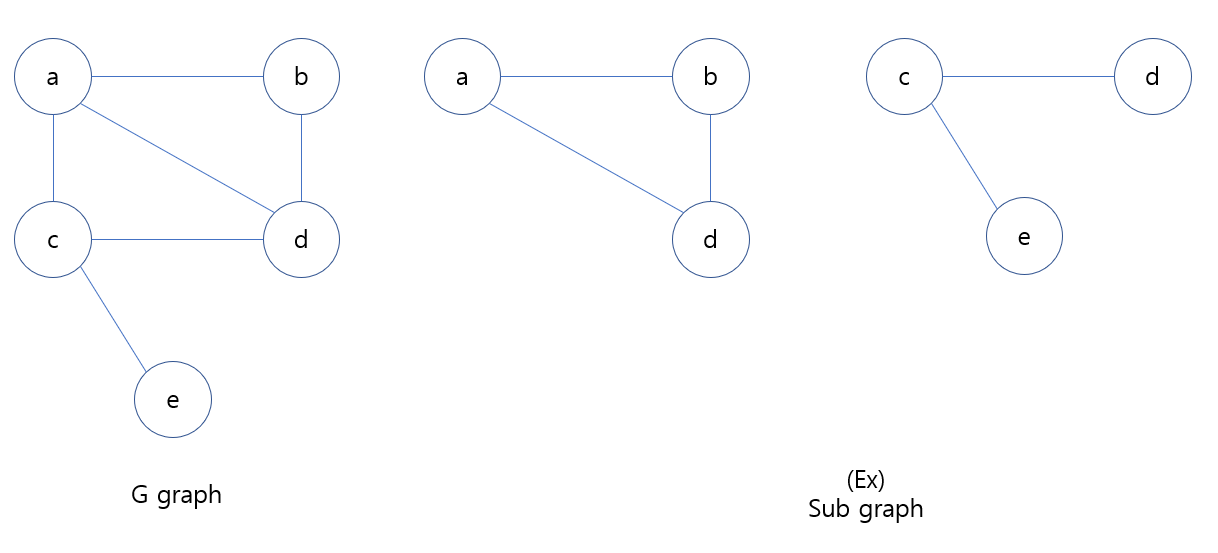
부분 그래프
부분 그래프(subgraph)는 그래프 G에서 V와 E로 주성된 그래프의 일부이다.
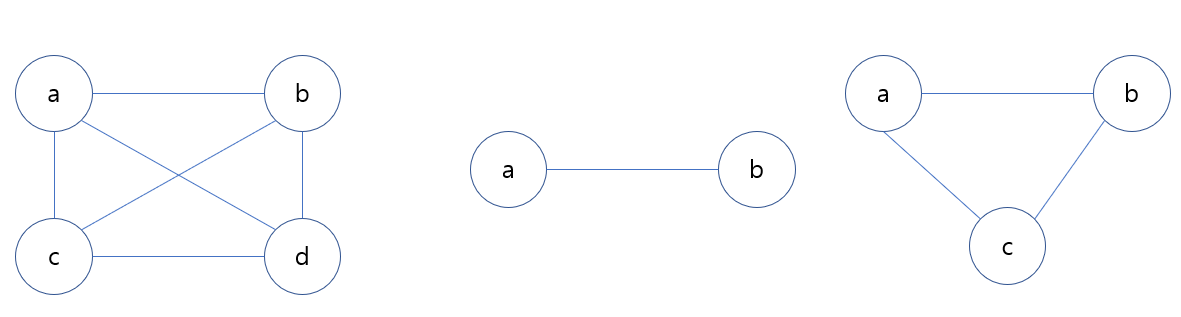
완전 그래프
완전 그래프(complete graph)는 그래프의 모든 노드가 서로 인접한 그래프를 말한다.
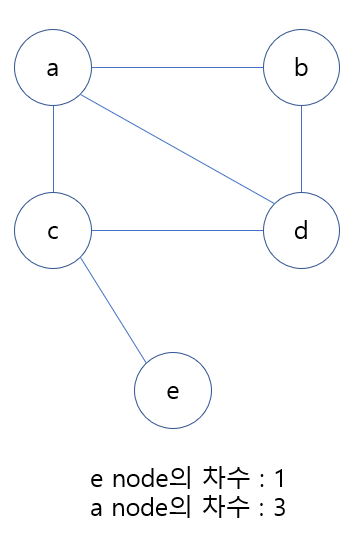
차수
차수(degree)는 한 노드에 이어져 있는 간선의 수.
차수가 0인 노드는 고립(isolated)되었다고 부른다. 방향이 없는 그래프는 입력 차수(in-degree)와 출력 차수(out-degree)로 나눌 수 있다.
이웃 함수
이웃 함수(neighborhood function)는 모든 이웃 V의 컨테이너다.
대표적으로 인접 리스트와 인접행렬을 많이 사용한다.
인접리스트(adjacency list)는 각 노드에서 이웃 리스트(set, dict, list etc..)에 접근할 수 있다.
여기서 예제에서는 list와 dict로 만들어보자.
리스트로 구현하면 어떤 알고리즘을 수행하는 작업이 이웃 노드를 반복해서 접근하는 경우 리스트를 사용하게 좋고, 간
선이 많은 경우 set을 이용하는 편이 좋다.
ex)
a,b,c,d,e,f = range(6) # node:6
N = [[b,c,d,f], [a,d,f], [a,b,d,e], [a,e], [a,b,d], [b,c,d,e]]
b in N[a] # True
b in N[b] # False
len(N[e]) # 차수 : 3
딕셔너리로 인접 리스트를 구현해보면 노드가 키가 되고, 각 노드를 간선 가중치 등의 값으로 연결할 수 있다.
ex)
a,b,c,d,e,f = range(6) # node:6
N = [{b:1,c:1,d:4,f:3}, {a:2,d:1,f:3}, {a:1,b:1,d:2,e:4}, {a:3,f:3}, {b:1, c:2, d:4, e:3}]
c in N[a] # True
len(N[d]) # 2
N[a][b] # 간선 가중치 1
인접행렬(adjacency matrix)은 각 노드의 모든 이웃에 대해 하나의 행를 갖는다.
각 행의 값은 True, False으로 이루어진다.
ex)
a,b,c,d,e,f = range(6) # node:6
N = [[1,1,0,0,0,1],[1,0,1,0,1,1],[1,1,1,1,0,0],[1,0,0,1,0,1],[1,1,1,0,0,0],[0,1,1,1,1,1,0]]
N[a][b] # 1
refernece : 파이썬 자료구조와 알고리즘
'02. Study > Algorithm' 카테고리의 다른 글
| DFS / BFS (0) | 2020.10.09 |
|---|---|
| Greedy Algorithm & Implementation (0) | 2020.10.07 |
| python_자료구조 (0) | 2019.08.31 |
| python_구조와 모듈 (0) | 2019.08.29 |
| python_(Set, Dictionary) (0) | 2019.08.28 |
